1.9K
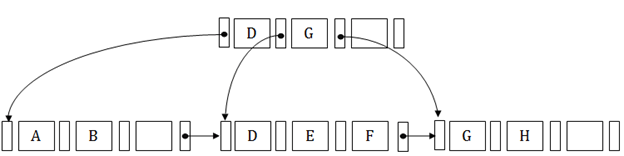
Structure of B+ Tree
Table of Contents
A B+ tree follows a multi-level index format and is a balanced binary search tree. A B+ tree’s leaf nodes denote actual data pointers. The B+ tree ensures that all leaf nodes stay balanced at the same height. In addition, a link list connects the leaf nodes; a B+ tree can therefore allow both random access and sequential access.
Structure of B+ Tree

Each node on the leaf is the same distance from the root node. For any B+ tree, a B+ tree is of the order n where n is fixed.
Internal nodes −
- Internal (non-leaf) nodes, except the root node, contain at least of [ n/2 ] pointers
- At most, n pointers may contain an internal nod
Leaf nodes −
- At least [ n/2 ] record pointers and [n/2] key values are stored in Leaf nodes.
- At most, n record pointers and n key values will contain a leaf node.
- Each node of the leaf contains a block pointer P to point to the next node of the leaf and forms a linked list.
B+ Tree Insertion
- From the bottom, B+ trees are filled and every entry is done at the leaf node.
- If a leaf node overflows −
- Split node into two parts.
- Partition at i = ⌊(m+1)/2⌋.
- First i entries are stored in one node.
- Rest of the entries (i+1 onwards) are moved to a new node.
- ith key is duplicated at the parent of the leaf.
- if a non-leaf node overflows −
- Split node into two parts.
- Partition the node at i = ⌈(m+1)/2⌉.
- Entries up to i are kept in one node.
- Rest of the entries are moved to a new node.
B+ Tree Deletion
- At the leaf nodes, B+ tree entries are deleted.
- The entry for the goal is searched and deleted.
- If it is an internal node, delete it from the left position and replace it with an entry.
- The underflow is tested after deletion,
- If there is an underflow, allocate the entries from the nodes left over.
- If distribution from the left is not possible, then
- Distributing right to it from the nodes.
- If distribution from the left or from the right is not feasible, then
- Merge to the left and right of the node.