B-tree

Table of Contents

In this article, you’ll learn about what is B-tree, why B-tree is used, it’s properties and Operations like Searching and B-Tree Applications.

What is B-tree ?

A B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time.

The B-tree generalizes the binary search tree, allowing for nodes with more than two children. Unlike other self-balancing binary search trees. It is also known as a height-balanced m-way tree.

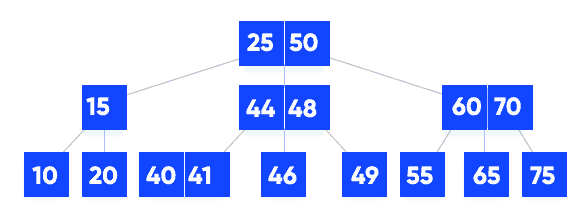
Why B-tree?

The need for B-tree arose with the rise in the need for lesser time in accessing the physical storage media like a hard disk. The secondary storage devices are slower with a larger capacity. There was a need for such types of data structures that minimize the disk accesses.
Other data structures such as a binary search tree, avl tree, red-black tree, etc can store only one key in one node. If you have to store a large number of keys, then the height of such trees becomes very large and the access time increases.
The B-tree is well suited for storage systems that read and write relatively large blocks of data, such as disks. It is commonly used in databases and file systems.
However, B-tree can store many keys in a single node and can have multiple child nodes. This decreases the height significantly allowing faster disk accesses.

B-tree Properties

For each node x, the keys are stored in increasing order.
In each node, there is a boolean value x.leaf which is true if x is a leaf.
If n is the order of the tree, each internal node can contain at most n – 1 keys along with a pointer to each child.
Each node except root can have at most n children and at least n/2 children.
All leaves have the same depth (i.e. height-h of the tree).
The root has at least 2 children and contains a minimum of 1 key.
If n ≥ 1, then for any n-key B-tree of height h and minimum degree t ≥ 2, h ≥ log_t (n+1)/2.

Operations

Searching

Searching for an element in a B-tree is the generalized form of searching an element in a Binary Search Tree. The following steps are followed.

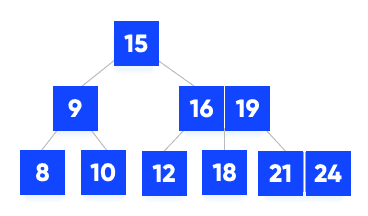
Searching Example

Let us search key k = 18 in the tree below of degree 3.

k is not found in the root so, compare it with the root key.

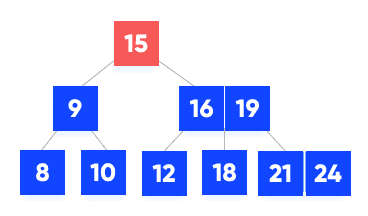
Since k > 15, go to the right child of the root node

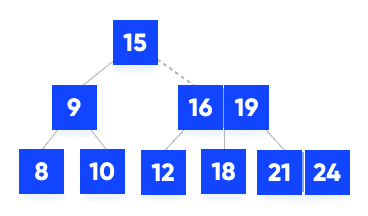
Compare k with 16. Since k > 16, compare k with the next key 19.

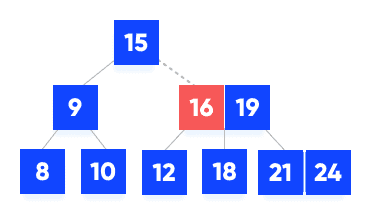
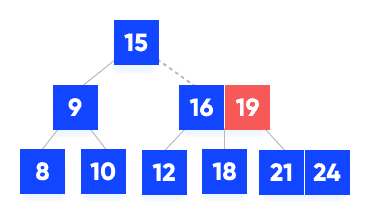
Since k < 19, k lies between 16 and 19. Search in the right child of 16 or the left child of 19.

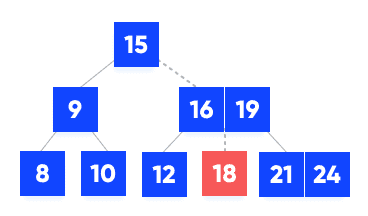
k is found

Algorithm for Searching an Element

BtreeSearch(x, k)
 i = 1
 while i ≤ n[x] and k ≥ keyi[x]        // n[x] means number of keys in x node
    do i = i + 1
if i  n[x] and k = keyi[x]
    then return (x, i)
if leaf [x]
    then return NIL
else
    return BtreeSearch(ci[x], k)

Searching Complexity on B Tree

Worst-case Time complexity: Θ(log n)
Average-case Time complexity: Θ(log n)
Best-case Time complexity: Θ(log n)
Average-case Space complexity: Θ(n)
Worst case Space complexity: Θ(n)

B Tree Applications

databases and file systems
to store blocks of data (secondary storage media)
multilevel indexing

C Examples

// Searching a key on a B-tree in C

#include <stdio.h>
#include <stdlib.h>

#define MAX 3
#define MIN 2

struct BTreeNode {
  int val[MAX + 1], count;
  struct BTreeNode *link[MAX + 1];
};

struct BTreeNode *root;

// Create a node
struct BTreeNode *createNode(int val, struct BTreeNode *child) {
  struct BTreeNode *newNode;
  newNode = (struct BTreeNode *)malloc(sizeof(struct BTreeNode));
  newNode->val[1] = val;
  newNode->count = 1;
  newNode->link[0] = root;
  newNode->link[1] = child;
  return newNode;
}

// Insert node
void insertNode(int val, int pos, struct BTreeNode *node,
        struct BTreeNode *child) {
  int j = node->count;
  while (j > pos) {
    node->val[j + 1] = node->val[j];
    node->link[j + 1] = node->link[j];
    j--;
  }
  node->val[j + 1] = val;
  node->link[j + 1] = child;
  node->count++;
}

// Split node
void splitNode(int val, int *pval, int pos, struct BTreeNode *node,
         struct BTreeNode *child, struct BTreeNode **newNode) {
  int median, j;

  if (pos > MIN)
    median = MIN + 1;
  else
    median = MIN;

  *newNode = (struct BTreeNode *)malloc(sizeof(struct BTreeNode));
  j = median + 1;
  while (j <= MAX) {
    (*newNode)->val[j - median] = node->val[j];
    (*newNode)->link[j - median] = node->link[j];
    j++;
  }
  node->count = median;
  (*newNode)->count = MAX - median;

  if (pos <= MIN) {
    insertNode(val, pos, node, child);
  } else {
    insertNode(val, pos - median, *newNode, child);
  }
  *pval = node->val[node->count];
  (*newNode)->link[0] = node->link[node->count];
  node->count--;
}

// Set the value
int setValue(int val, int *pval,
           struct BTreeNode *node, struct BTreeNode **child) {
  int pos;
  if (!node) {
    *pval = val;
    *child = NULL;
    return 1;
  }

  if (val < node->val[1]) {
    pos = 0;
  } else {
    for (pos = node->count;
       (val < node->val[pos] && pos > 1); pos--)
      ;
    if (val == node->val[pos]) {
      printf("Duplicates are not permitted\n");
      return 0;
    }
  }
  if (setValue(val, pval, node->link[pos], child)) {
    if (node->count < MAX) {
      insertNode(*pval, pos, node, *child);
    } else {
      splitNode(*pval, pval, pos, node, *child, child);
      return 1;
    }
  }
  return 0;
}

// Insert the value
void insert(int val) {
  int flag, i;
  struct BTreeNode *child;

  flag = setValue(val, &i, root, &child);
  if (flag)
    root = createNode(i, child);
}

// Search node
void search(int val, int *pos, struct BTreeNode *myNode) {
  if (!myNode) {
    return;
  }

  if (val < myNode->val[1]) {
    *pos = 0;
  } else {
    for (*pos = myNode->count;
       (val < myNode->val[*pos] && *pos > 1); (*pos)--)
      ;
    if (val == myNode->val[*pos]) {
      printf("%d is found", val);
      return;
    }
  }
  search(val, pos, myNode->link[*pos]);

  return;
}

// Traverse then nodes
void traversal(struct BTreeNode *myNode) {
  int i;
  if (myNode) {
    for (i = 0; i < myNode->count; i++) {
      traversal(myNode->link[i]);
      printf("%d ", myNode->val[i + 1]);
    }
    traversal(myNode->link[i]);
  }
}

int main() {
  int val, ch;

  insert(8);
  insert(9);
  insert(10);
  insert(11);
  insert(15);
  insert(16);
  insert(17);
  insert(18);
  insert(20);
  insert(23);

  traversal(root);

  printf("\n");
  search(11, &ch, root);
}