RSA Algorithm

In this article you’ll learn about (Rivest–Shamir–Adleman) RSA Algorithm and implementation of RSA algorithm using C program.

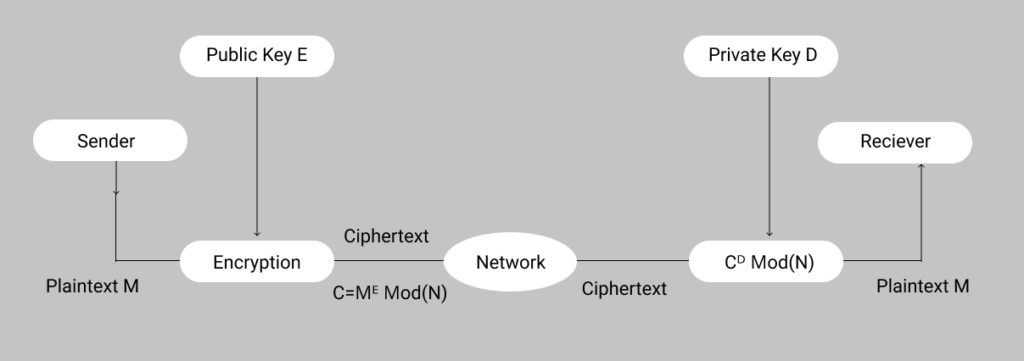
RSA algorithm is an asymmetric cryptography algorithm. Asymmetric actually means that it works on two different keys i.e. Public Key and Private Key. As the name describes that the Public Key is given to everyone and the Private key is kept private.

The principle of RSA is based upon the fact that if it is easy to multiply two prime numbers but it is very difficult to factor the product and get them back.

The algorithm is as follows :

1. Take two very large prime number A and B of equal lengths and obtain their product (N).Therefore,

N=AXB

2. Subtract 1 from A as well as B and take the product T.Therefore ,

T=(A-1)(B-1)

3. Choose the product public key E which is a randomly chosen number such that it has no common factors with T.

4. Obtain the private Key (D) as under :

D=E^-1 Mod(T)

5. The rule for encryption of a block of plaintext M into ciphertext(C) is as under:

C= M^E Mod(N)

6. The received message C at the receiver is decrypted to obatin the plaintext back by using the following rule ,

M =C⁰ Mod(N)

C implementation of RSA algorithm for small values:

// C program for RSA asymmetric cryptographic
// algorithm. For demonstration values are
// relatively small compared to practical
// application
#include<stdio.h>
#include<math.h>

// Returns gcd of a and b
int gcd(int a, int h)
{
	int temp;
	while (1)
	{
		temp = a%h;
		if (temp == 0)
		return h;
		a = h;
		h = temp;
	}
}

// Code to demonstrate RSA algorithm
int main()
{
	// Two random prime numbers
	double p = 3;
	double q = 7;

	// First part of public key:
	double n = p*q;

	// Finding other part of public key.
	// e stands for encrypt
	double e = 2;
	double phi = (p-1)*(q-1);
	while (e < phi)
	{
		// e must be co-prime to phi and
		// smaller than phi.
		if (gcd(e, phi)==1)
			break;
		else
			e++;
	}

	// Private key (d stands for decrypt)
	// choosing d such that it satisfies
	// d*e = 1 + k * totient
	int k = 2; // A constant value
	double d = (1 + (k*phi))/e;

	// Message to be encrypted
	double msg = 20;

	printf("Message data = %lf", msg);

	// Encryption c = (msg ^ e) % n
	double c = pow(msg, e);
	c = fmod(c, n);
	printf("\nEncrypted data = %lf", c);

	// Decryption m = (c ^ d) % n
	double m = pow(c, d);
	m = fmod(m, n);
	printf("\nOriginal Message Sent = %lf", m);

	return 0;
}

OUTPUT

Message data = 12.000000 
Encrypted data = 3.000000 
Original Message Sent = 12.000000